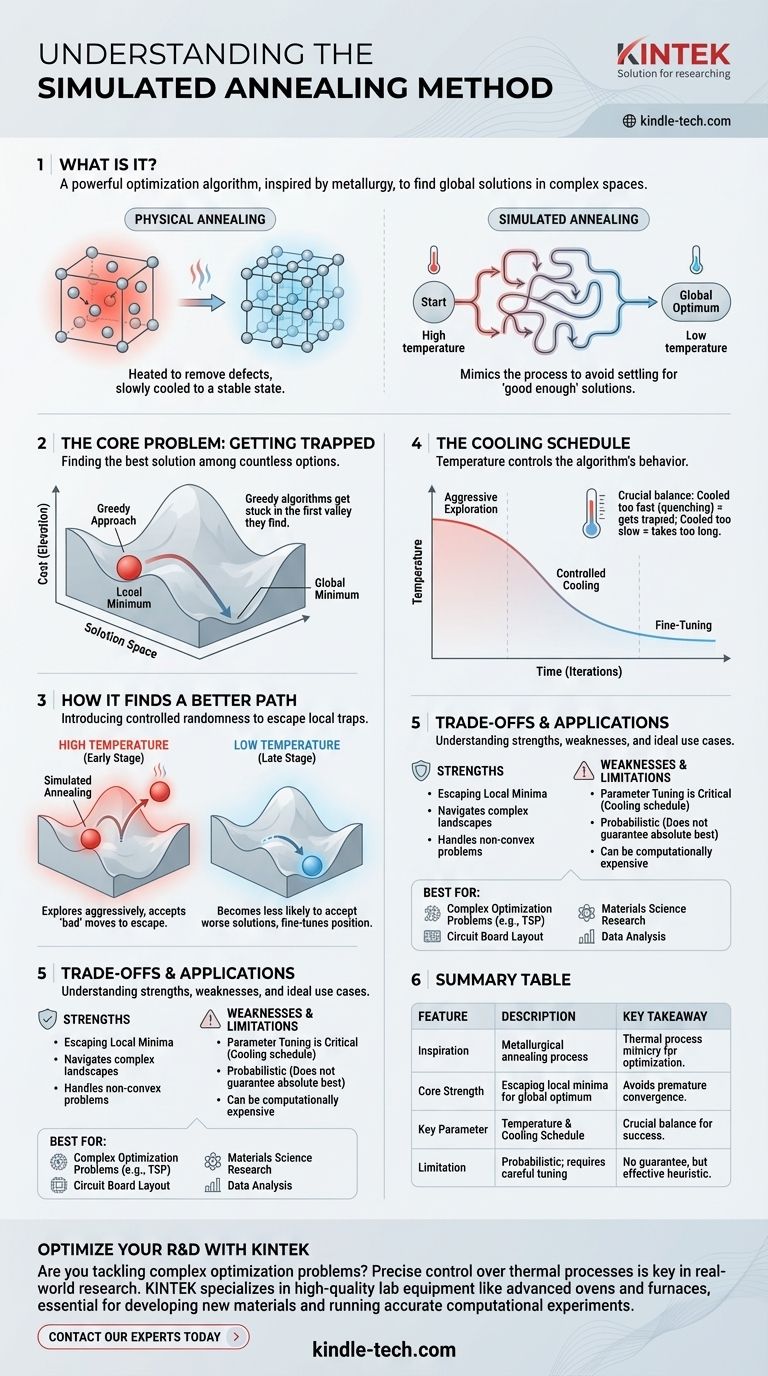
简而言之,模拟退火是一种强大的优化算法,用于在广阔而复杂的搜索空间中找到一个好的(通常是全局)解决方案。它直接受到冶金退火过程的启发,在该过程中,材料被加热然后缓慢冷却,以消除缺陷并达到稳定的、低能量的晶态。该算法模仿这一物理过程来解决抽象的计算问题。
模拟退火的核心在于,它通过模仿金属退火的物理过程,避免了满足于“足够好”的解决方案的常见陷阱。它首先探索广泛的可能性(高温),然后逐渐缩小范围,聚焦于高质量、稳定的解决方案(低温)。
核心问题:陷入困境
要理解模拟退火,您必须首先理解它所解决的问题:在无数选项中找到最佳解决方案,这项任务被称为优化。
解决方案的景象
想象一下,您问题的每一个可能解决方案都是一个广阔、起伏不平的景观上的一个点。每个点的高度代表其“成本”——高度越低,解决方案越好。您的目标是找到整个地图上最低的点,即全局最小值。
“贪婪”方法及其缺陷
一个简单的算法,通常称为爬山法,会从一个随机点开始,并始终向下移动。这是一种“贪婪”方法,因为它只接受能立即带来改进的移动。
问题在于,这种方法会陷入它找到的第一个山谷——一个局部最小值。它无法知道在下一座山后面是否存在一个更深的山谷,即全局最小值。

模拟退火如何找到更好的路径
模拟退火通过引入受控的随机性元素来克服这一限制,使其能够逃离这些局部陷阱。
灵感来源:物理退火
在冶金学中,加热金属会使其原子获得足够的能量自由移动,从而摆脱次优的、有缺陷的结构。当金属缓慢冷却时,原子有时间沉降成高度有序、坚固的晶格——一种最低能量状态。
算法:温度作为控制旋钮
模拟退火通过引入一个温度参数来采用这一概念。这不是一个物理温度,而是一个控制算法行为的变量。
算法从高温开始。在这种状态下,它会积极地探索解决方案空间,就像热金属中充满活力的原子一样。它接受比当前位置更差的移动的概率很高。这是关键:进行“糟糕”的移动正是它能够爬出局部最小值的关键。
冷却时间表
随着算法的运行,温度会根据冷却时间表逐渐降低。随着温度的降低,算法接受更差解决方案的可能性越来越小。
最终,在极低的温度下,算法的行为就像简单的爬山法,只接受改进并微调其位置,希望达到全局最小值。
理解权衡
像任何强大的工具一样,模拟退火并非万能解决方案。理解其局限性对于有效使用它至关重要。
优点:逃离局部最小值
它的主要优势在于能够驾驭具有许多局部最小值的复杂、非凸景观。对于贪婪算法始终失败的问题,模拟退火是一个绝佳的选择。
缺点:参数调整至关重要
算法的性能对冷却时间表高度敏感。如果冷却过快,它仍然可能陷入局部最小值(“淬火”)。如果冷却过慢,找到解决方案可能需要不切实际的时间。找到合适的计划通常需要实验。
局限性:它是一种概率方法
模拟退火不能保证它会找到绝对最佳解决方案(全局最小值)。它是一种启发式方法,这意味着它旨在在合理的时间内找到一个非常好的解决方案。它总是有统计学上的机会停留在次优状态。
为您的项目做出正确选择
使用本指南来决定模拟退火是否是您优化任务的正确方法。
- 如果您的主要重点是解决一个有许多陷阱(局部最小值)的复杂问题:模拟退火是最好的工具之一,特别是对于旅行商问题或电路板布局等经典问题。
- 如果您的主要重点是以最快速度找到可证明的最佳解决方案:您应该首先检查您的问题是否足够简单(例如,凸),可以通过更快的确定性算法(如线性规划或标准贪婪方法)来解决。
最终,模拟退火提供了一个强大的框架,用于在广阔而困难的搜索空间中导航,以在更简单方法失败时找到高质量的解决方案。
总结表:
| 特征 | 描述 |
|---|---|
| 灵感来源 | 冶金退火过程(加热和缓慢冷却) |
| 核心优势 | 逃离局部最小值以找到全局最优解 |
| 关键参数 | 温度和冷却时间表 |
| 最适合 | 具有许多局部陷阱的复杂优化问题 |
| 局限性 | 概率性;需要仔细调整参数 |
使用 KINTEK 优化您的研发
您是否正在材料科学、化学工程或数据分析领域应对复杂的优化问题?模拟退火的原理受到真实世界热过程的启发,在您的实验室中精确控制这些过程至关重要。
KINTEK 专注于高质量的实验室设备,包括先进的烘箱和炉子,它们提供研发所需的均匀加热和受控冷却。无论您是开发新材料还是进行计算实验,可靠的设备都是准确结果的基础。
立即联系我们的专家,找到完美的实验室解决方案,以增强您的优化工作流程并取得突破性成果。
图解指南