简而言之,更大的样本量不会改变测量仪器的固有准确性,但它会极大地提高您可以从数据中得出的结论的准确性。 通过收集更多样本,您可以减少“抽样误差”,即仅观察群体的一部分而非整体所带来的不确定性。这意味着您的结果更有可能成为整个群体的真实代表。
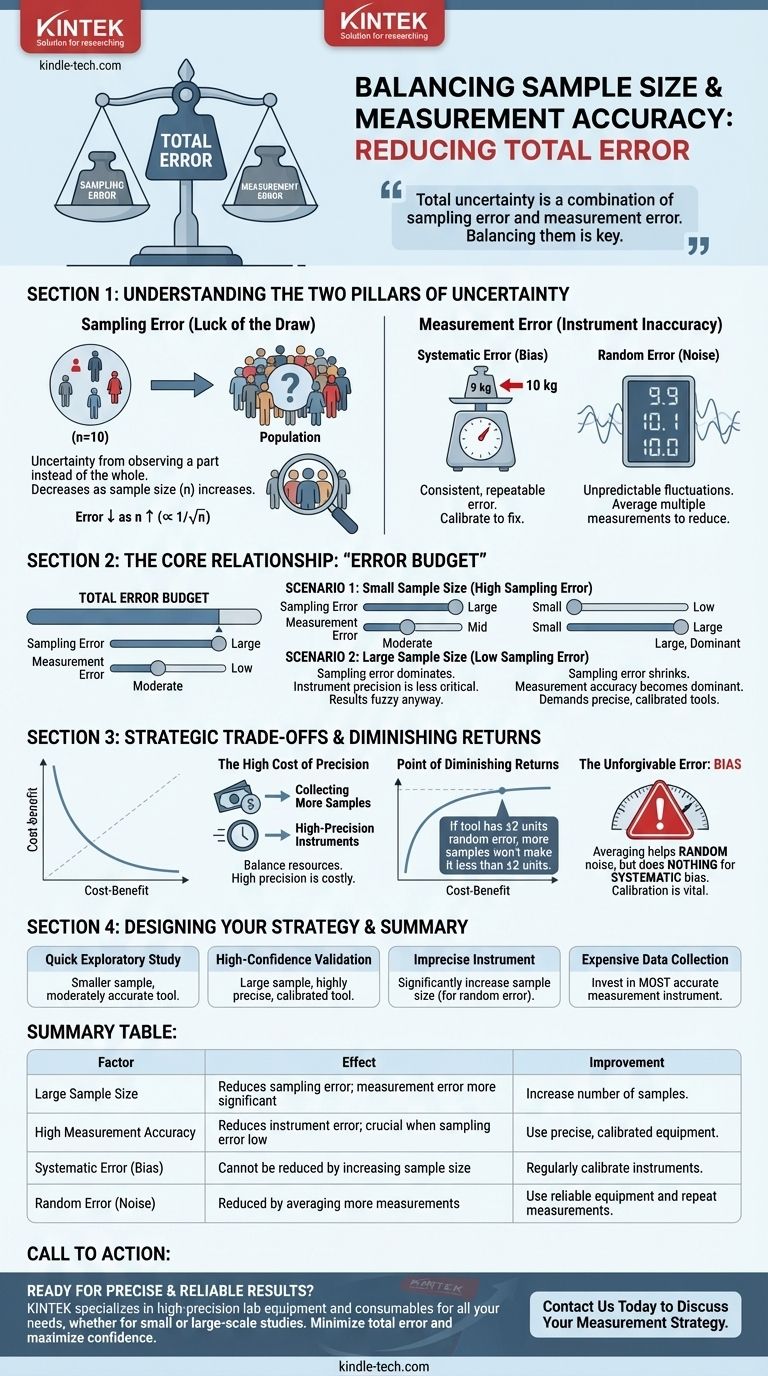
核心问题不仅仅是样本量;而是要平衡两种不同的误差来源。您的总不确定性是抽样误差(来自样本大小)和测量误差(来自工具质量)的组合。了解这两者如何相互作用是设计有效研究的关键。
不确定性的两大支柱:抽样与测量
要充分理解这种关系,您必须区分可能影响结果的两种基本类型的误差。它们是不可互换的。
理解抽样误差
抽样误差是“随机性”问题。它是您的样本特征与它所代表的整个群体特征之间的随机差异。
想象一下,您试图通过仅测量 10 个人来确定一个城市所有人的平均身高。您可能会偶然选择一个异常高或异常矮的群体。
这种误差不是错误;它是一个统计现实。好消息是它是可预测的,并且可以控制。随着您的样本量 (n) 增加,您的抽样误差会以与样本量平方根 (1/√n) 成正比的速度减小。更大的样本更有可能反映真实的人群。
理解测量误差
测量误差是测量设备或方法中固有的不准确性。它与您抽取多少样本无关。
这种误差有两种形式:
- 系统误差(偏差): 一种一致的、可重复的误差。想象一个秤总是读数高出 1 公斤。测量更多次数不会解决这个问题;您只会得到一个非常精确但错误的答案。
- 随机误差(噪声): 测量中不可预测的波动。想象一个数字秤的最后一位数字略有闪烁。
平均多次测量有助于减少随机误差的影响,但它永远无法纠正系统误差。您工具的准确性为您数据的最终真实性设定了硬性限制。

样本量和测量准确性如何相互作用
关键的见解是,这两种误差共同构成了您的总“误差预算”。您的目标是最小化总误差,而您如何分配资源来对抗每种类型的误差取决于您的情况。
核心关系:“误差预算”
将您期望的置信水平视为总误差的预算。您将此预算“花费”在抽样误差和测量误差的组合上。
如果一种误差源非常大,它将主导您的结果,而减小另一种误差源可能几乎没有实际效果。
情景 1:小样本量
当您的样本量很小时,抽样误差很高。它几乎总是您总不确定性的最大贡献者。
在这种情况下,测量工具的精度就不那么重要了。无论如何,由于抽样中的“随机性”,您的结果都会很模糊,因此少量的测量误差不会使整体情况变得更糟。
情景 2:大样本量
随着样本量的增加,抽样误差急剧缩小。您的样本平均值越来越接近真实的人群平均值。
这就是用户的问题变得特别有见地的地方。大样本量有效地提高了对准确测量的要求。随着抽样误差的消失,来自仪器的任何误差都成为不确定性的主要来源。
如果您的测量工具有系统偏差,巨大的样本量只会给您一个错误的数值的非常精确的估计。它放大了拥有经过良好校准和准确仪器的重要性。
理解权衡
决定样本量和仪器质量是一项战略性的平衡行为,通常受时间和金钱的制约。
精度的昂贵代价
收集更多样本会花费时间和资源。同样,高精度、完美校准的仪器也很昂贵。您必须决定在哪里投入。
如果您的结果最终受到廉价、不准确的测量工具的限制,那么投入巨额资金用于庞大的样本量是浪费的。
边际效益递减点
存在一个点,增加样本量几乎没有好处。如果您的测量工具具有 ±2 单位的固有随机误差,无论您进行多少次测量,您都无法达到小于该值的最终置信区间。
同样,如果您只计划进行三次测量,购买价值数百万美元的仪器是毫无意义的,因为您巨大的抽样误差将使仪器的惊人精度相形见绌。
不可原谅的错误:偏差
请记住,增加样本量有助于平均随机噪声,但对修复系统偏差没有任何作用。
无论样本量如何,校准您的仪器以消除系统误差通常是您可以采取的确保数据完整性的最重要的一步。
设计您的测量策略
不存在单一的“正确”样本量或准确度级别。正确的选择完全取决于您的目标和限制。
- 如果您的主要重点是快速的探索性研究: 较小的样本量结合中等准确度的仪器可能足以识别主要趋势并指导未来的研究。
- 如果您的主要重点是高置信度验证(例如,监管批准): 您需要一个大且经过仔细选择的样本,以及一个高精度、经过校准的仪器,以将抽样误差和测量误差减少到可验证的程度。
- 如果已知您的测量仪器不精确: 您可以通过显著增加样本量来弥补,但这仅适用于误差是随机的,而不是系统的。这将减少您的总体不确定性,但仅限于仪器缺陷设定的限制。
- 如果收集样本极其昂贵或困难(例如,太空探索): 您必须投资于最准确的测量仪器,以便从每一份宝贵的数据点中提取最大价值。
最终,平衡样本量和测量准确性在于战略性地分配您的资源,以应对您特定情况下不确定性的最主要来源。
总结表:
| 因素 | 对结果的影响 | 如何改进 |
|---|---|---|
| 大样本量 | 减少抽样误差;使测量误差更显著。 | 增加测量的样本数量。 |
| 高测量准确性 | 减少仪器误差;在抽样误差低时至关重要。 | 使用精确、校准良好的设备。 |
| 系统误差(偏差) | 增加样本量无法减少。 | 定期校准仪器。 |
| 随机误差(噪声) | 可以通过平均更多测量值来减少。 | 使用可靠的设备并重复测量。 |
准备好在您的实验室中获得精确可靠的结果了吗?
样本量和测量准确性的正确平衡对于您数据的完整性至关重要。KINTEK 专注于高精度实验室设备和耗材,满足您的所有实验室需求。无论您是需要具有卓越准确性的小样本集仪器,还是需要用于大规模研究的强大设备,我们都有解决方案来最小化您的总误差并最大化您发现的置信度。
立即联系我们,讨论我们的产品如何增强您的测量策略。让我们专业的专家帮助您为您的特定应用选择最合适的工具。
图解指南